Finite Element Modeling of Rat Optic Nerve Head Biomechanics (Stephen Schwaner)
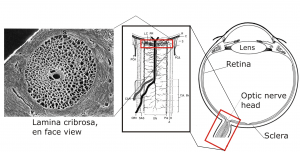
Glaucoma is the second leading cause of blindness worldwide, and is characterized by the death of retinal ganglion cells (RGC) which carry vision information to the brain [1]. A key risk factor in glaucoma is elevated intraocular pressure (IOP). Elevated IOP induces mechanical stress and strain in the tissues of the optic nerve head (ONH), which is thought to contribute to retinal ganglion cell axon insult. The ONH is a region in the posterior eye with complex tissue morphology, including a passage in the sclera (connective tissue shell of the eye) known as the scleral canal. RGC axons pass through a web of connective tissue (lamina cribrosa) that spans this canal as they exit the eye and converge to form the optic nerve (Figure 1).
Figure 1: From left to right: electron microscopic image of the lamina cribrosa, schematic of the ONH, and schematic of the eye anatomy [2]. All three represent human anatomy.
Although data suggest that mechanical insult to the ONH could be a key driver in the glaucomatous process leading to RGC death, the complicated relationship between the two is not well understood [3]. Animal models are utilized by researchers to characterize this relationship. One such model is the rat, a widely-used and well-accepted glaucoma model. After induction of elevated IOP, the rat ONH presents with similar damage patterns compared to those seen in human glaucoma [4 – 7]. However, there are significant structural differences between the human and rat ONH which will likely affect rat ONH biomechanics [7].
Therefore, our goal is to characterize rat ONH biomechanics by using finite element analysis (FEA). FEA is a mechanical engineering technique that produces computer models used to calculate stress and strain in complicated mechanical systems. We will look for patterns of stress and strain predicted by our models and compare them with patterns of damage and cell death observed in experimental rat studies. In this way, the FE models that we create will provide a needed biomechanical framework for interpreting results drawn from the rat model of glaucoma. Ultimately, we hope that this work will provide a useful tool for improving our understanding of the relationship between biomechanics and RGC death in glaucoma.
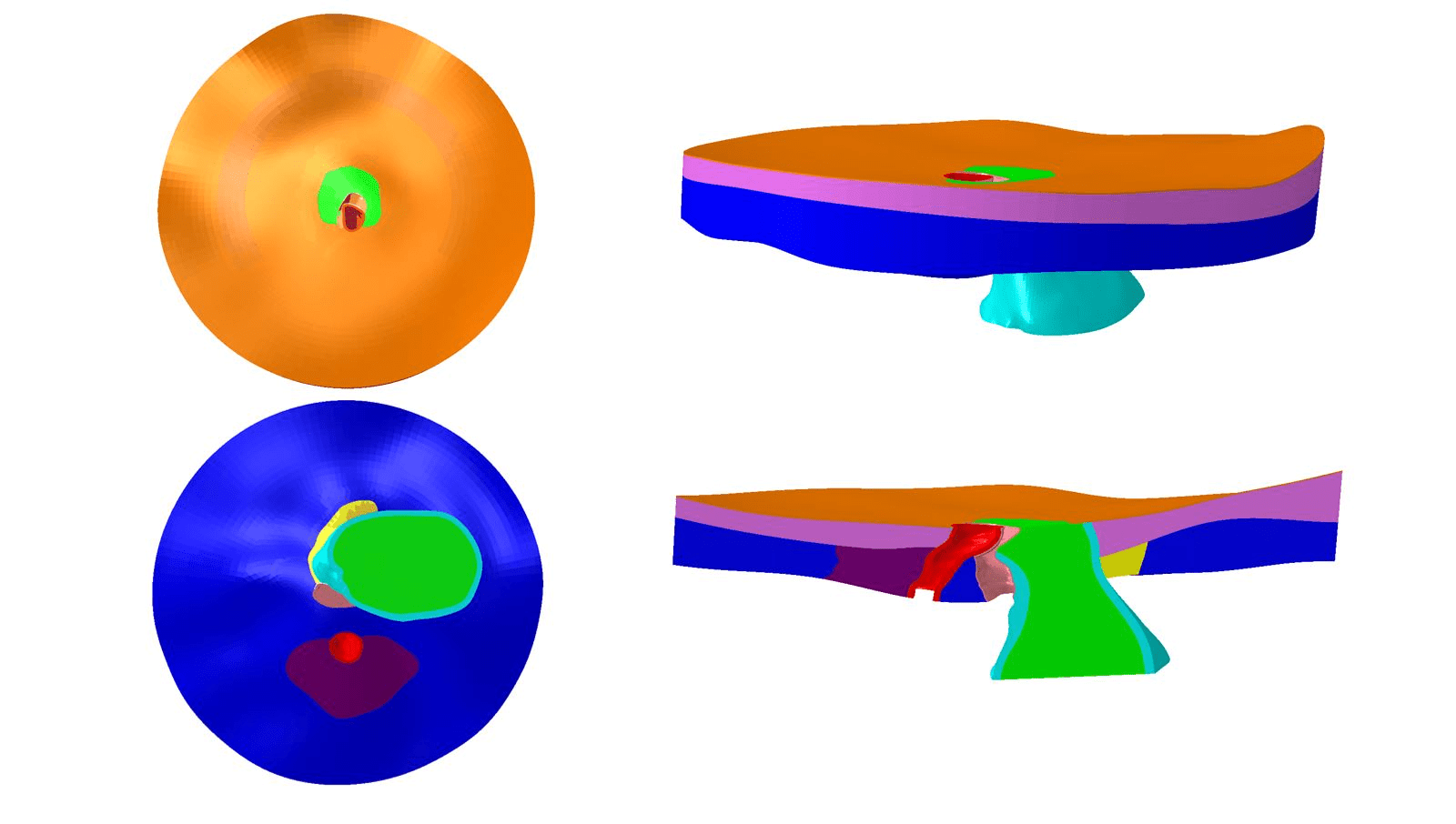
Through a collaboration with the labs led by Drs. Claude Burgoyne and John Morrison in Portland, Oregon, we have been given point cloud data sets describing rat ONH tissue geometries [8]. We are using these data sets to build individual-specific rat ONH FE models (Figure 2). We also plan to utilize experimental techniques to measure the mechanical properties of rat ONH tissues, which we will then use as parameters in our FE models.
Figure 2: Top view (top left), bottom view (bottom left), side view (top right), and side cut view (bottom right) of a rat ONH finite element model geometry.
1. Varma, R., et al., An assessment of the health and economic burdens of glaucoma. Am. J. Ophthalmol., 2011. 152(4): p. 515-522.
2. Ethier, CR and Simmons, CA, Introductory Biomechanics: From Cells to Organisms, Cambridge University Press, 2007.
3. Burgoyne, CF, A biomechanical paradigm for axonal insult within the optic nerve head in aging and glaucoma. Exp. Eye Res., 2011. 93(2): p. 120-132.
4. Johnson, E. et al., Chronology of the optic nerve head and retinal responses to elevated intraocular pressure. Invest. Ophthalmol. Vis. Sci., 2000. 41(2): p. 431-432.
5. Guo, L., et al., Retinal ganglion cell apoptosis in glaucoma is related to intraocular pressure and IOP-induced effects on extracellular matrix. Invest. Ophthalmol. Vis. Sci., 2005. 46(1): p. 175-182.
6. Pease, M.E., et al., Obstructed axonal transport of BDNF and its receptor TrkB in experimental glaucoma. Invest. Ophthalmol. Vis. Sci., 2000. 41(3): p. 764-774.
7. Morrison J.C., et al., A rat model of chronic pressure-induced optic nerve damage. Exp. Eye Res., 1997. 64(1): p. 85-96.
8. Pazos, M. and Yang, H. et al., Rat optic nerve head anatomy within 3D histomorphometric reconstructions of normal control eyes. Exp. Eye Res., 2015. 139: p. 1-12.